maandag 31 maart 2014
Life is full of misery...
Woody Allen - Quotes of the Day
zaterdag 29 maart 2014
Wiswijzer
Vooruitgang
Robert Heinlein - Quotes of the Day
Onzekerheid
Ursula K. LeGuin - Quotes of the Day
zondag 23 maart 2014
Work in progress
Losse eindjes:
- Kernbegrippen
- Rekenvaardigheid
- Vakinhoudelijk
- Vakdidactiek voor dummies
- Work in progress
- Vakwerkplan HAVO/VWO
Meer in algemene zin:
- De inzet van ICT
- Wat is rekenen?
zaterdag 22 maart 2014
Wiskunde: vaardigheden, begrip en inzicht
Zie ook Wiskunde: vaardigheden, begrip en inzicht
Zinloos getwitter
- Ik heb vandaag een goed gesprek gehad met @huppeldepup...
Wat moet je daar mee? Moet de hele wereld weten dat je kennelijk in staat bent een goed gesprek te voeren? Waar ging dat dan over? Kunnen wij daar misschien iets van leren? Mogen we weten waar het over ging misschien?
- Vandaag hebben we een hele inpirerende bijeenkomst gehad....
Meestal met een foto erbij, maar waar het nu over ging? Hebben we iets gemist? Hadden we er bij moeten zijn dan? Moeten die mensen niet werken? Kunnen we nog ergens de opbrengsten vinden van die bijeenkomst? Dat, zeg maar, de mensen die er niet waren er misschien ook iets aan zouden kunnen hebben? Of wil je alleen maar even laten weten dat je goed bezig bent?
- Bedankt voor je e-mail. Ik heb het plaatje opgeslagen...
Ja... leuk... communiceren via twitter over e-mail... en ook bedankt... Ik weet alleen niet zo goed waarvoor... Was het leuk? Interessant voor anderen misschien? Of was het geheim? Schokkend? Niet voor iedereen geschikt?
- Heeft er iemand voor mij informatie/lesmateriaal over ...
Lekker makkelijk. Zeker te lui om zelf te zoeken of om iets zelf te maken. Je roept iets en dan hopen dat je van alles krijgt toegeworpen? Dat kan natuurlijk wel, maar doe je dat zelf dan ook? Of ben je meer van het nemen dan van het geven?
- RT Ik vind het boekje van @huppeldepub erg interessant...
Elke vermelding van je boekje op Twitter retweeten is natuurlijk wel een mogelijkheid. Maar na een tijdje wordt het vervelend. Ok, je hebt een boekje geschreven en je bent succesvol. Dan mag je best trots zijn, maar je moet niet overdrijven.
- ... people unfollowed me
Tja... dat verbaast me niks. Ik vraag me dan altijd af waarom zou je dat willen weten? Sommigen mensen volgen je en anderen stoppen er mee. Nou en? Moet je daar iets mee? Wat is je doel? Zo veel mogelijk volgers? En dan? Ga je dan zinnige dingen roepen? Ik weet het niet...
- Ik ben bij Albert Heijn op de huppeldepupstraat...
Dat is boeiend. Is daar iets te beleven dan? Moeten wij je nu op komen zoeken? De GGD bellen? De politie alarmeren? Of juist vooral de andere kant op lopen...
- Ik heb zojuist 20 meter gelopen in 0:31:22 uur...
Nou ja.. zoiets dan... Knap hoor. 't Is maar goed dat we daarvan op de hoogte zijn. Ik weet niet precies wat ik daar mee moet, maar vooruit maar. Goed bezig.
Nu ja, je begrijpt het al. Er is weliswaar veel informatie beschikbaar, maar wat nu precies de bedoeling is van al die inhoudsloze berichten? De wereld laten weten dat je lekker bezig bent? Laten weten dat je er bent? Laten weten dat er dingen zijn die verder niemand kan zien? Dingen roepen om de onderlinge verbondenheid te versterken? Je vlaggen zetten?
Dat kan allemaal, maar ik weet alleen niet of ik daar nu op zit te wachten...
Gelukkig zijn er ook veel mensen die aardige dingen delen waar je wel iets aan hebt, waar je iets van kan leren of iets anders mee kan. Soms hebben ze dat niet echt zelf bedacht, maar vaak ook wel.
Dat laatste is verreweg het aardigst, vind ik...:-)
Geïrriteerd? Wat doe je er aan?
Dat lijkt eenvoudiger dan het is. Je wilt op de hoogte blijven, altijd bang dat je iets mist...? Maar dat is onwaarschijnlijk. Je hoeft echt niet bang te zijn dat je iets mist. Als het belangrijk is dan ontkom je er toch niet aan, zo niet dan was het ook niet belangrijk. Het is niet nodig om je aan dingen te ergeren. Dat heb je zelf in de hand. Uiteindelijk kan je je beter richten op de dingen waar je energie van krijgt.
Hoe moeilijk kan dat zijn?:-)
donderdag 20 maart 2014
Gemeenteraadsverkiezing Den Haag
De definitieve uitslag van de gemeenteraadsverkiezingen van de gemeente Den Haag wordt op vrijdag 21 maart om 10.00 uur bekendgemaakt tijdens de zitting van het Hoofdstembureau.
maandag 17 maart 2014
De Hond: D66 wordt de grootste in Den Haag
bron
Leerstijlen maar dan anders
- de dienstweigeraar
- de ontdekkingsreiziger
- de lijnentrekker
- de denker
't Is gewoon een truuk...
Er ging zo maar iemand roepen:
| Zie en huiver: wiskunde zonder enig begrip en inzicht |
Is dat zo? Of is dit een voorbarige conclusie?
1e voorbeeld:
(a+2)(a-5)=a(a-5)+2(a-5)=a2-5a+2a-10=a2-3a-10
2e voorbeeld:
(a-2)(a-5)=a(a-5)-2(a-5)=a²-5a-2a+10=a²-7a+10
Mooier kan je 't niet verzinnen:-)
Maar is dat nu heel anders dan Hoe werk je dubbele haakjes weg? Dat lijkt me niet...
Wat voor de een een truuk is is voor de ander volstrekt helder. Als je denkt dat het een truuk is dan begrijp je 'm gewoon niet. 't Is geen truuk. Zo is de staartdeling ook geen truuk. Maar 'lijnentrekkers' noemen dat een truuk omdat ze niet echt begrijpen hoe het in elkaar zit.
Maar wat voor een 'onzin' iemand ook roept er is altijd nog wel iemand die het er helemaal mee eens is. Lijntrekken als modetrend? Treuriger kan het bijna niet worden...
zondag 16 maart 2014
zaterdag 15 maart 2014
De rekentoets
Algebra nieuwe stijl
Een voorbeeld uit TAAK 61:
Daar kan je nu niet meer mee aan komen...:-) Of misschien toch wel...
In plaats van allerlei nieuwe boeken te maken met dezelfde soort sommetjes, kunnen ze dit soort boekjes gewoon weer opnieuw uitgeven. Over ronddraaien in cirkeltjes gesproken. Deze is ook nog wel aardig:
Misschien dat zoiets nog wel beter werkt ook nog...
bron:
taakboeken voor het technisch onderwijs
2
nieuwe stijl
ALGEBRA
N.W.Velders
Leraar N.O. en Pedagogiek M.O. te Amsterdam
J.B. Wolters Groningen 1964
vrijdag 14 maart 2014
Verhaaltjes, contexten, toepassingen en modellen
In de praktijk blijkt dat wiskundedocenten in de les zich zo snel mogelijk ontdoen van `contexten` en `verhaaltjes`. Iemand die het gras moet maaien is niet interessant... het gaat om het berekenen van de oppervlakten. Dat grasmaaien was mogelijkerwijs bedoeld om `het probleem` in een herkenbare context te plaatsen, zodat het probleem minder abstract is en leerlingen zich er gemakkelijker iets bij kunnen voorstellen. Hoop je dan...
Het is niet zo heel moeilijk om de `gezochtheid` van allerlei `contexten`, `neptoepassingen` en `verhaaltjes` aan te tonen. Wiskunde is tenslotte abstract en alle pogingen om er iets van te maken wat realistisch overkomt? Ik denk dat wiskundedocenten daar niet veel heil in zien. Dat `realistische reken- en wiskundeonderwijs` is toch maar onzin eigenlijk...
Het is niet zo gek dat leerlingen het idee dat al die `verhaaltjes` eigenlijk maar een beetje onzin zijn van hun wiskundeleraren overnemen. In dat geval is de basis van het dat zgn. realistische reken- en wiskundeonderwijs wel zo`n beetje onderuit gehaald.
Wel de `oude wiskunde` afgeschaft maar niet de `nieuwe wiskunde` ingevoerd? Dan zitten we met een slap aftreksel van herinneringen aan vroeger en dromen van een toekomst die nog niet begonnen is. |
Maar bij opgaven is de `context` natuurlijk wel belangrijk. Bij het behangprobleem speelt het feit dat over `behang` gaat en niet bijvoorbeeld over `verf` wel een rol en dan vooral voor het afronden.
Eigenlijk kan je veel realistische rekenopgaven beschouwen als voorbeelden van modelleren. Er is een `probleem`, je vertaalt het probleem naar `wiskunde`, je lost het `wiskundige probleem` op en je vertaalt de uitkomst naar het `probleem`:
Af en toe krijg je `t gevoel dat veel mensen gewoon af willen van dat modelleren en terugvertalen. Leer eerst rekenen en wiskunde, geen flauwekul, gewoon optellen en vermenigvuldigen, delen en breuken, vergelijkingen oplossen, haakjes wegwerken, haakjes maken, kwadraatafsplitsen, ontbinden in factoren, enz.
Waarschijnlijk ligt daar het fundamentele misverstand. Wat is rekenen? Wat is wiskunde? Is dat gewoon heel veel 'domme sommen' maken of zou er toch nog iets meer achter zitten?:-)
donderdag 13 maart 2014
Goed of fout
bron
dinsdag 11 maart 2014
Hersenen
Robert Frost - Quotes of the Day
maandag 10 maart 2014
Dat doe je gewoon zo en zo...
Dertien tafeltennissers spelen een halve competitie. Dat betekent dat elke speler precies één keer speelt tegen elke ander speler. Hoeveel wedstrijden worden er in totaal gespeeld?Op Wedstrijden heb ik nog 's een poging gedaan om te laten zien hoe je dat aan zou kunnen pakken. Nu is de vraag 'wat zou je nu willen dat leerlingen daarvan onthouden?'.
Je kunt dit uit je hoofd leren en de meeste leerlingen zullen daar geen moeite mee hebben. Je moet het dan wel onthouden, maar, je begrijpt al, na een aantal weken zou er zo maar verwarring kunnen ontstaan... 'Moest je eerst het kwadraat nemen en dan delen door twee?', 'Hoe zat het nu ook alweer precies?'. 't Is een leuk idee, maar niet iets dat echt blijft hangen misschien.
Je kunt je zelfs afvragen of het kunnen uitrekenen van het aantal wedstrijden nu het doel was van de lessen. Misschien was die 'competitie' wel gewoon een 'context' om telproblemen aan te pakken. Dus die hele of halve competitie kan ons eigenlijk niet veel schelen.... nee het gaat om aanpakken van een telprobleem. Maak 's een plaatje en beredeneer hoeveel wedstrijden er gespeeld worden.
Als je daar wat verder over nadenkt... Wat is eigenijk het doel van wiskundeonderwijs? Zou het aanpakken van problemen, het redeneren, e.d. niet een veel hoger goed zijn dan het kunnen oplossen van vooraf vastgestelde trivialiteiten die je (mits je over de juiste vaardigheden beschikt) een fluitje van een cent zijn...
Je meer kunnen richten op mee algemene vaardigheden die ook nog 's bredere inzetbaar zijn zou toch wel mooi zijn.:-)
zaterdag 8 maart 2014
De kapitein
- Hoe pak je nu zoiets aan?
Er geldt dan:
2s + k = 49
k - s = 2s - k
Het verschil in leeftijd verandert immers niet. Oplossen van het stelsel geeft: k = 21 en s = 14, dus de kapitein is nu 28 jaar oud.
Oefening 1
Jan is vandaag jarig. Precies 12 jaar geleden was zijn moeder 4 keer zo oud als hij. Nu is zij nog maar 2 keer zo oud als Jan.
- Hoe oud was zijn moeder toen Jan werd geboren?
Lennard is 32 jaar en twee keer zo oud als Willemien was toen hij zo oud was als zij nu is.
- Hoe oud is Willemien?
vrijdag 7 maart 2014
Pilot CITO rekentoets 3F van 2013
bron
Hieronder zie je een overzichtje van de slechts gemaakt vragen de 3F toets:
(c) Willem van Ravenstein - voorbeeld rekentoets 3F van CITO van 2013
Tafeltennis
Vraag 38 uit de CITO-voorbeeldrekentoets 3F van 2013 is slecht gemaakt. HAVO 12% goed en VWO 29% goed:
AANPAK
Er zijn verschillende mogelijkheden om dit aan te pakken. Je zou kunnen beredeneren dat elk speler 12 wedstrijden moet spelen. Maar als je \(13\times12\) doet dan speelt iedereen twee keer tegen elkaar (dat is een hele competitie), dus moet je nog delen door twee. Er worden \(\large\frac{13\times 12}{2}\)=\(78\) wedstrijden gespeeld.
De halve competitie komt ook voor in het wiskundeboek voor de tweede klas. Dat lijkt, in 't algemeen, geen problemen op te leveren. Maar kennelijk is het niet zo vanzelfsprekend als je zou denken, gezien de resultaten.
Duidelijk is in ieder geval dat de manier waarop je dit soort problemen aan zou kunnen pakken (rooster, graaf, tellen...) niet echt is blijven hangen. Dat is ook wel een soort thema bij de rekentoets. Allerlei vaardigheden die op een bepaald moment in de schoolloopbaan geen enkel probleem zijn blijken later te zijn vergeten, onbegrepen, weggezakt... Wat een treurigheid...
Dit was voorlopig de laatste vraag in de serie 'slechtstgemaakte vragen van de rekentoets'. Deze vragen staan op een rijtje bij de resultaten. Er zijn ook verwijzingen naar WisFaq.
donderdag 6 maart 2014
Intervaltraining
Hoe pak je dat aan?
't Is in het begin wel even puzzelen hoe dat nu precies zit, maar 't komt neer op:
- 6 kilometer intervaltraining bestaat uit 5 keer hardlopen (5 km) en 5 keer wandelen (1 km).
- In totaal duurt dat 37 minuten.
- De wandelsnelheid is 5 km per uur, dus 1 km wandelen duurt 12 minuten.
- 5 km hardlopen in 25 minuten is \(\frac{1}{5}\) km/minuut.
- De gemiddelde snelheid bij 't hardlopen is 60 · \(\frac{1}{5}\) =12 km/uur.
Bij probleemaanpak (HAVO 4 wiskunde B) heb ik de opgave gebruikt als één van de problemen. In de 'hints' heb ik toen gekozen voor een wiskundige aanpak:
- De hardloopsnelheid is \(v\) en de wandelsnelheid is \(5\).
- Reken dan uit hoeveel
uur hij er over doet.
Er geldt: \(\large\frac{5}{v} + \frac{1}{5} = \frac{{37}}{{60}}\). - Oplossen geeft \(v=12\)
In de komende weken zal ik nog 's wat vaker kijken naar de resultaten van de CITO voorbeeldrekentoets. Wat waren de moeilijke vragen? En waarom?
Versnelling
Hoe pak je dat aan?
- Als de trapas 1000 keer rond gaat dan gaat het achterwiel 3000 keer rond.
- De diameter is 68 cm. De omtrek is 3,14 · 68 = 213,52 cm.
- De afgelegde weg is 3000 · 213,52 = 640.560 cm
- Dat is ongeveer 6,4 km.
In de komende weken zal ik nog 's wat vaker kijken naar de resultaten van de CITO voorbeeldrekentoets. Wat waren de moeilijke vragen? En waarom?
Tour de France
HAVO: 9% VWO: 29%:
Hoe pak je dat aan?
De snelheid is gelijk aan de afstand gedeeld door de tijd. Het gaat hier om de snelheid in kilometer per uur, dus je moet het aantal kilometers delen door het aantal uur. De afstand is 15 km. De tijd is 19 minuten, 32 seconden en dan nog 51 seconden, dus 19 minuten en 83 seconden. Maar hoeveel uur is dat? Het aantal minuten moet je dan delen door 60 en het aantal seconden door 3600, dat tel je op en dan weet je de tijd in uren.
-
Wat is de afstand?
De afstand is 15 km. -
Wat is de tijd?
De tijd is 19 minuten en 83 seconden. -
Hoeveel uur is 19 minuten en 83 seconden?
Dat is 0,33972 uur. - Deel 15 door 0,33972... en je krijgt 44,15372... km/uur.
- Afronden op 1 decimaal geeft dan 44,2 km/uur.
- 15/(19/60+83/3600) = 44,2 km/uur
In de komende weken zal ik nog 's wat vaker kijken naar de resultaten van de CITO voorbeeldrekentoets. Wat waren de moeilijke vragen? En waarom?
woensdag 5 maart 2014
Bollen
Hoe pak je dit aan?
Misschien is het handig om een schets te maken?
- Elke bol heeft een vierkantje nodig van 10x10 cm.
- Bij 1,50 m bij 1,80 m kan je dan 15×18=270 bollen kwijt.
Verzin 't maar 's... De diepere bedoeling van deze vraag ontgaat me, eerlijk gezegd, een beetje. Wat zou hier worden getoetst? Probleemaanpak? IQ? Iets anders?
In de komende weken zal ik nog 's wat vaker kijken naar de resultaten van de CITO voorbeeldrekentoets. Wat waren de moeilijke vragen? En waarom?
Kunstwerk
Hoe pak je dat aan?
Om de aankoopsprijs in 1986 te kunnen vergelijken met de verkoopsprijs in 2009 moet je verkoopsprijs in euro omrekenen in dollar. De vraag is immers 'met hoeveel dollar...'. Als je de verkoopsprijs in dollar hebt dan kan je de winst uitrekenen.
- Bereken de verkoopsprijs in dollar.
- Bereken de winst (verkoopsprijs - aankoopsprijs)
- Bereken het aantal jaren van 1986 naar 2009.
- Bereken de toename per jaar.
- Rond af op duizendtallen.
- De verkoopsprijs in dollar is 32.700.000×1,34 = 43.818.000 dollar
- De winst is gelijk aan 43.818.000 - 385.000 = 43.433.000 dollar
- Het aantal jaren is 2009 - 1986 = 23
- De toename per jaar is 43.433.000 : 23 = 1.888.391,30 dollar
- Afgerond op duizendtallen is dat 1.888.000 dollar per jaar.
Er begint zich zo langzamerhand wel een patroon te ontwikkelen, geloof ik. Alweer minimaal 5 evidente stappen te nemen. Een foutje is snel gemaakt... dat is wederom vragen om moeilijkheden.
Op zich is het wel een leuk probleem. Je koopt een kunstwerk voor slechts $385.000 en wat denk je? Na 23 jaar verkoop je de handel en dan hoef je verder nooit meer te werken, geen dingen te doen waar je geen zin hebt en vooral geen rekentoets te doen. Ergens doe ik iets niet goed...:-)
Maar kennelijk ben ik NIET de enige...:-(
De vraag was op WisFaq ook een keer langsgekomen:
In de komende weken zal ik nog 's wat vaker kijken naar de resultaten van de CITO voorbeeldrekentoets. Wat waren de moeilijke vragen? En waarom?
dinsdag 4 maart 2014
Aantal verkochte fietsen
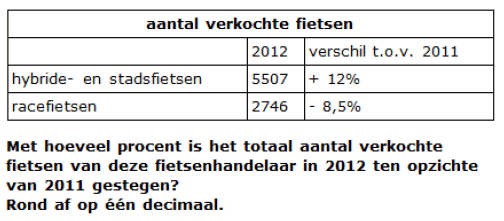
Hoe pak je dat aan?
Om het aantal verkochte fietsen van 2011 en 2012 te kunnen vergelijken moet je weten hoeveel fietsen er in 2011 en in 2012 verkocht zijn. Het aantal verkochte fietsen in 2012 gaat nog wel, maar het aantal in 2011 is nog even een puzzel.
- aantal hybride- en stadsfietsen in 2011 is gelijk aan 5507 : 1,12 = 4917
- aantal racefietsen in 2011 is gelijk aan 2746 : 0,915 = 3001
- totaal aantal verkochte fietsen in 2011 is dan 4917 + 3001 = 7918
- totaal aantal verkochte fietsen in 2012 is 5507 + 2746 = 8253
- procentuele toename is gelijk aan (8253-7918):7919×100% = 4,2%
Je hoeft geen groot 'toetsdeskundige' of 'professor' te zijn om te begrijpen dat dit vragen om moeilijkheden is. Hoe meer stappen hoe groter de kans op een foutje, maar dan is wel de hele vraag fout.
Waarschijnlijk is stap 2. de lastige stap. Groeifactoren dus... Zo'n opstapeling van moelijkheden is niet nodig. Je kunt al deze stappen heel gemakkelijk apart toetsen, maar kennelijk is het bedoeling om te toetsen of leerlingen ook 5 (lastige) stappen perfect kunnen doorlopen?
Uiteindelijk zegt het weinig als een leerling deze vraag fout heeft. Alleen stap 2. misschien fout gedaan? Of de laatste stap? Of de vraag helemaal niet begrepen? Of zelfs niet eens een poging gedaan? Ik weet het niet, dat moet beter kunnen....
10% van de HAVO-leerlingen en 30% van de VWO-leerlingen hadden deze vraag goed. Dat had natuurlijk niemand kunnen zien aankomen...:-(
In de komende weken zal ik nog 's wat vaker kijken naar de resultaten van de CITO voorbeeldrekentoets. Wat waren de moeilijke vragen? En waarom?
De werkelijkheid
Jane Wagner - Quotes of the Day
maandag 3 maart 2014
Aandelen
Hoe pak je dat aan?
Deze vraag bestaat uit twee delen:
- Je koopt 200 aandelen die per stuk €9,60 kosten. Daarbij moet je nog transactiekosten betalen. De transactiekosten zijn 0,8% van de totale waarde van de aandelen. Die moet je dan nog apart betalen.
- Je verkoopt 200 aandelen voor €17,20 per stuk. Nu moet je ook transactiekosten betalen. Deze kosten gaan dan af van het bedrag wat je krijgt voor de aandelen.
- Je hebt betaald: 200·9,60·1,008 = €1935,36
- Je krijgt terug: 200·17,20·0,991 = €3409,04
- Trek (1) van (2) af. Je winst is €1473,68 euro.
- 200·17.20·0.991-200·9.60·1.008 = €1473.68
Op WisFaq was de vraag ook al 's aan de orde geweest. Kennelijk is een minimale aanwijzing over het 'verhaaltje' voldoende om het te kunnen uitrekenen. Maar waar zijn we dan mee bezig? Is dat begrijpend lezen of rekenen?
In de komende weken zal ik nog 's wat vaker kijken naar de resultaten van de CITO voorbeeldrekentoets. Wat waren de moeilijke vragen? En waarom?
Proefpartij tegels
Hoe pak je zoiets aan?
De tegels kosten €12,90 per m², maar hoeveel vierkante meter heb je? Het zijn 1800 tegels van 42x42cm. De hoogte doet er niet toe.
Rekenen in meter geeft een totale oppervlakte van 0,42×
- Wat is de totale oppervlakte in m²?
- Bereken de totale prijs.
- Rond af op honderdtallen.
Meer stappen betekent meer kans op een foutje... maar 'een klein foutje' is net zo fout als complete onzin.
In de komende weken zal ik nog 's wat vaker kijken naar de resultaten van de CITO voorbeeldrekentoets. Wat waren de moeilijke vragen? En waarom?
Schaatser
Hoe pak je zoiets aan?
Als je km in minuten wilt vergelijken met meter in seconden dan moet je of km/min omrekenen naar m/ s of m/s naar km/min. In de vraag gaat het om seconden, dus reken kilometer in minuten om naar meter in seconden.
stap 1
10 km = 10.000 m
15 minuten = 900 seconden
stap 2
Als je 10.000 meter in 900 seconden wilt 'omrekenen' naar 400 meter dan gebruik je een verhoudingstabel.
| 10.000 m | 400 m |
| 900 sec | ? |
Je kunt kruislings vermenigvuldigen en dan kijken naar het verschil met 37,7 seconden.
Wat leerlingen zouden moeten leren zijn o.a. dit soort algemene noties over wat 'handig' is. Als je dingen wilt vergelijken gebruik dan dezelfde eenheden, kijk naar de eenheden van het gevraagde antwoord en het gebruik verhoudingstabellen.
Zie ook Hoeveel seconden?
In de komende weken zal ik nog 's wat vaker kijken naar de resultaten van de CITO voorbeeldrekentoets. Wat waren de moeilijke vragen? En waarom?
zondag 2 maart 2014
Vrijdag de 13e

HAVO scoort 28% en VWO scoort 35%. Dat is wel erg weinig. Ik weet niet precies wat dit met rekenen te maken heeft, maar dit was mijn antwoord:
 13 februari is vrijdag
13 februari is vrijdag13 maart is zaterdag
20 maart is zaterdag
27 maart is zaterdag
28 maart is zondag
29 maart is maandag
30 maart is dinsdag
31 maart is woensdag
1 april is donderdag
't Is gewoon een kwestie van even uitschrijven. Dat kan vast ook intelligenter, maar 't geeft mij in ieder geval voldoende zekerheid dat het antwoord klopt.
Het roept in ieder geval een aantal vragen op:
- Wat heeft dit met 'rekenen' te maken?
- Wat wordt hier eigenlijk getoetst?
- Waarom wordt, zelfs door VWO-leerlingen, deze vraag zo slecht gemaakt?
zaterdag 1 maart 2014
Mijn documenten
| Mijn documenten | |
Jaartal
|
Aantal
|
2008
|
2
|
2009
|
122
|
2010
|
223
|
2011
|
253
|
2012
|
126
|
2013
|
151
|
2014
|
76
|
953
| |
't Was niet zo gek dat ik nooit iets terug kon vinden.:-)
The real me
Peter Sellers - Quotes of the Day