Wiswijzer+

zaterdag 18 maart 2023

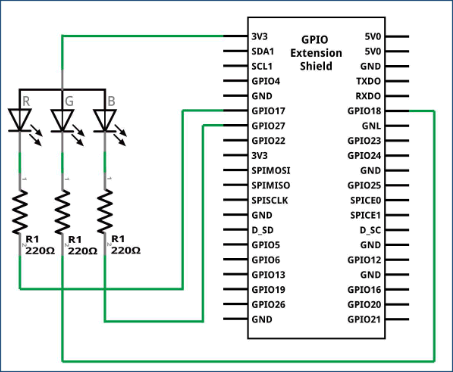
Beep

import RPi.GPIO as GPIO
import time

# Set #17 as buzzer pin
BeepPin = 17

def print_message():
    print ("========================================")
    print ("|                 Beep                 |")
    print ("|    ------------------------------    |")
    print ("|        Buzzer connect to GPIO0       |")
    print ("|                                      |")
    print ("|            Make Buzzer beep          |")
    print ("|                                      |")
    print ("|                                      |")
    print ("========================================\n")
    print ('Program is running...')
    print ('Please press Ctrl+C to end the program...')

def setup():
    # Set the GPIO modes to BCM Numbering
    GPIO.setmode(GPIO.BCM)
    # Set LedPin's mode to output, 
    # and initial level to High(3.3v)
    GPIO.setup(BeepPin, GPIO.OUT, initial=GPIO.HIGH)

def main():
    print_message()
    while True:
        # Buzzer on (Beep)
        print ('Buzzer On')
        GPIO.output(BeepPin, GPIO.LOW)
        time.sleep(0.1)
        # Buzzer off
        print ('Buzzer Off')
        GPIO.output(BeepPin, GPIO.HIGH)
        time.sleep(0.1)

def destroy():
    # Turn off buzzer
    GPIO.output(BeepPin, GPIO.HIGH)
    # Release resource
    GPIO.cleanup()    

# If run this script directly, do:
if __name__ == '__main__':
    setup()
    try:
        main()
    # When 'Ctrl+C' is pressed, the child program 
    # destroy() will be  executed.
    except KeyboardInterrupt:
        destroy()

zondag 12 maart 2023

vrijdag 3 maart 2023

Fractal Music

Een fractaal muziekstuk is opgebouwd uit eenheden die dezelfde structuur hebben als het gehele muziekstuk.

Speel een stukje fractal music voor de jury. Het mag ritmisch en/of melodisch zijn, naast stemmen wordt het gebruik van muziekinstrumenten toegejuicht.

Presentatie, kostumering en overgave leggen ook gewicht in de schaal.

Na afloop mag het teamlid dat de meeste structuur in zijn leven heeft aan de jury uitleggen waarom in het concert sprake was van fractal music.

Materiaal: Alles wat bruikbaar is.

bron

dinsdag 28 februari 2023

Willem van Ravenstein is een bekende wiskundeleraar en de oprichter van de website WisFAQ.nl⁵, waar hij vragen over wiskunde beantwoordt. Hij heeft ook een YouTube-kanaal³ waar hij wiskundelessen geeft. Hij heeft verschillende boeken over wiskunde geschreven⁴.

Willem van Ravenstein - Jan van Zanen. https://janvanzanen.denhaag.nl/willem-van-ravenstein/
Geopend 27-2-2023.
Willem van Ravenstein - YouTube. https://www.youtube.com/channel/UC7gWSuvGouW1R-cb2KR1h3w
Geopend 27-2-2023.
(PDF) Willem van Ravenstein - wiskundeleraar.nl · Moderne wiskunde .... https://dokumen.tips/documents/willem-van-ravenstein-moderne-wiskunde-vwo-bovenbouw-wiskunde-b1-deel.html
Geopend 27-2-2023.

Bron: Gesprek met Bing, 27-2-2023

donderdag 19 januari 2023

Apple TV

woensdag 18 januari 2023

Wat is wiswijzer?

"De website heeft als doel om individuen te helpen weloverwogen beslissingen te nemen en zich te redden in complexe situaties door duidelijke en onpartijdige informatie te bieden. Wiswijzer is een onafhankelijke organisatie en wordt gefinancierd door de overheid, goede doelen fondsen en andere sponsors."

chatGPT

maandag 9 januari 2023

CD55

zondag 8 januari 2023

50 meesterwerken der muziek

woensdag 4 januari 2023

Historisch

Minister van der Hoeven reageert in een interview met het Algemeen Dagblad op de protesten uit de Bèta-hoek:

"Met het imago dat het moeilijk is en zwaar, zoals wis en natuurkunde hebben, schiet een vak niks op. Een vak kan beter bekend staan als aantrekkelijk en de moeite waard om te kiezen."

Heel goed! Je kunt ook beter gezond en rijk zijn dan arm en ziek.

bron